Explore Group Theoretic Unification
Group theory is the study of mathematical groups, which are sets of elements combined by a binary operation that follows four rules: closure, associativity, the existence of an identity element, and the existence of an inverse for each element.
Group theory is a fundamental part of abstract algebra and is widely used to study symmetry in Mathematics, Physics, and Chemistry, as well as in areas like Cryptography and Topology.
The study of groups is not just limited to Mathematics, as it is also a subject in other fields, such as Political Science, Sociology, and others. Ifa Group Theory (IfaGPT) entails doing the subject of Group Theory in any field in Ifa Language (IfaLang).

Discover the Foundations of Ifa Group Theory
Delve into key Principles that unify mathematics and science through Ifa Group Theory.
Unifying Mathematical Structures
Understand how Ifa Group Theory integrates diverse mathematical frameworks.
Applications in Science
Examine the role of Ifa Group Theory in bridging scientific disciplines.
Technological Integration
Learn how this framework supports innovative technological advancements.
Future Directions
Explore emerging trends and research pathways in Ifa Group Theory.
Ancient Algebraic Structures: The 16 IfaGroups
The 16 Major Odu Ifa are the 16 Ifa Groups or ToE Groups. These Meta-Structures are also known as Ifa Identities or ToE Identities, the Ifa Laws of Nature governing all fields and disciplines.
The Ejiogbe Group

The Oyeku Meji Group

The Iwori Meji Group

The Odi Meji Group

The Irosun Meji Group

The Owonrin Meji Group

The Obara Meji Group

The Okanran Meji Group

The Ogunda Meji Group

The Osa Meji Group

The Ika Meji Group

The Oturupon Meji Group

The Otura Meji Group

The Irete Meji Group

The Ose Meji Group

The Ofun Meji Group

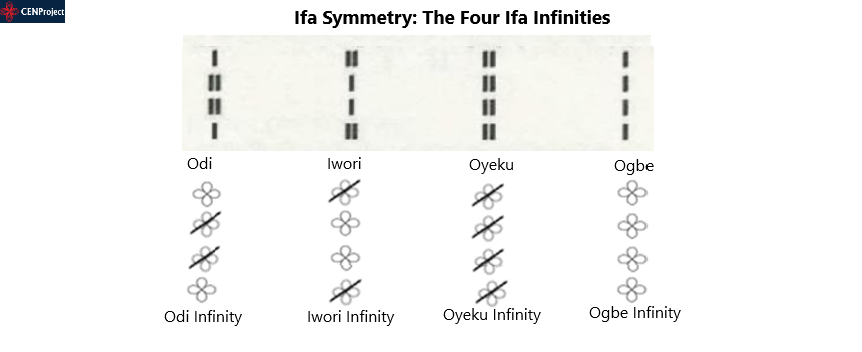
Ifa Symmetry
Symmetry in Ifa is a key area of study in Ifa Group Theory and Ifa Periodic Table. IfaSymmetry, the Symmetry of Everything (SymoE), involves studying symmetry in IfaLang, specifically focusing on the Four Symmetric Ifa Codes known as the Ifa Four: Ogbe Symmetry, Oyeku Symmetry, Iwori Symmetry, and Odi Symmetry:
Ifa Assymetry
There are 12 Major Assymetric Ifa Codes: Irosun, Owonrin, Obara, Okanran, Ogunda, Osa, Ika, Oturupon, Otura, Irete, Ose, Ofun.
Unlocking the Power of Ifa Group Theory
Discover how Ifa Group Theory unifies mathematics and science, providing innovative frameworks for complex problems.
Ifa Symmetry
Use Ifa Fractal to study the Symmetry for Everything (SymoE), IfaSymmetry, as a knowledge integration and unification Tool.
Cross-Disciplinary Integration
See how Ifa Group Theory bridges gaps between scientific and non-scientific disciplines, fostering collaboration and technological advancement.
Innovative Applications
Learn how the group-theoretic approach transforms complex systems into manageable models with real-world impact.

Dive Deep into the Foundations of Group Theory
Engage with cutting-edge insights into Ifa Group Theory to unify knowledge across all disciplines.
